Workshop

Introduction to statistical models: Single linear regression

Introduction

In this workshop you will get practice in applying, interpreting and reporting single linear regression.

Artwork by Horst (2023): “linear regression dragons”

Session overview

In this session you will carry out, interpret and report on a single linear regression.

Philosophy

Workshops are not a test. It is expected that you often don’t know how to start, make a lot of mistakes and need help. It is expected that you are familiar with independent study content before the workshop. However, you need not remember or understand every detail as the workshop should build and consolidate your understanding. Tips

• don’t worry about making mistakes
• don’t let what you can not do interfere with what you can do
• discussing code with your neighbours will help
• look things up in the independent study material
• look things up in your own code from earlier
• there are no stupid questions

Key

These four symbols are used at the beginning of each instruction so you know where to carry out the instruction.

Something you need to do on your computer. It may be opening programs or documents or locating a file.

Something you should do in RStudio. It will often be typing a command or using the menus but might also be creating folders, locating or moving files.

Something you should do in your browser on the internet. It may be searching for information, going to the VLE or downloading a file.

A question for you to think about and answer. Record your answers in your script for future reference.

Getting started

Start RStudio from the Start menu.

Go the Files tab in the lower right pane and click on the ... on the right. This will open a “Go to folder” window. Navigate to a place on your computer where you keep your work. Click Open.

Make an RStudio project for this workshop by clicking on the drop-down menu on top right where it says Project: (None) and choosing New Project, then New Directory, then New Project. Navigate to the data-analysis-in-r-1 folder and name the RStudio Project week-6.

Make new folders called data-raw and figures. You can do this on the Files Pane by clicking New Folder and typing into the box that appears.

Make a new script then save it with a name like single-linear-regression.R to carry out the rest of the work.

Add a comment to the script: # Introduction to statistical models: Single linear-regression and load the tidyverse (Wickham et al. 2019) package

Exercises

Linear Regression

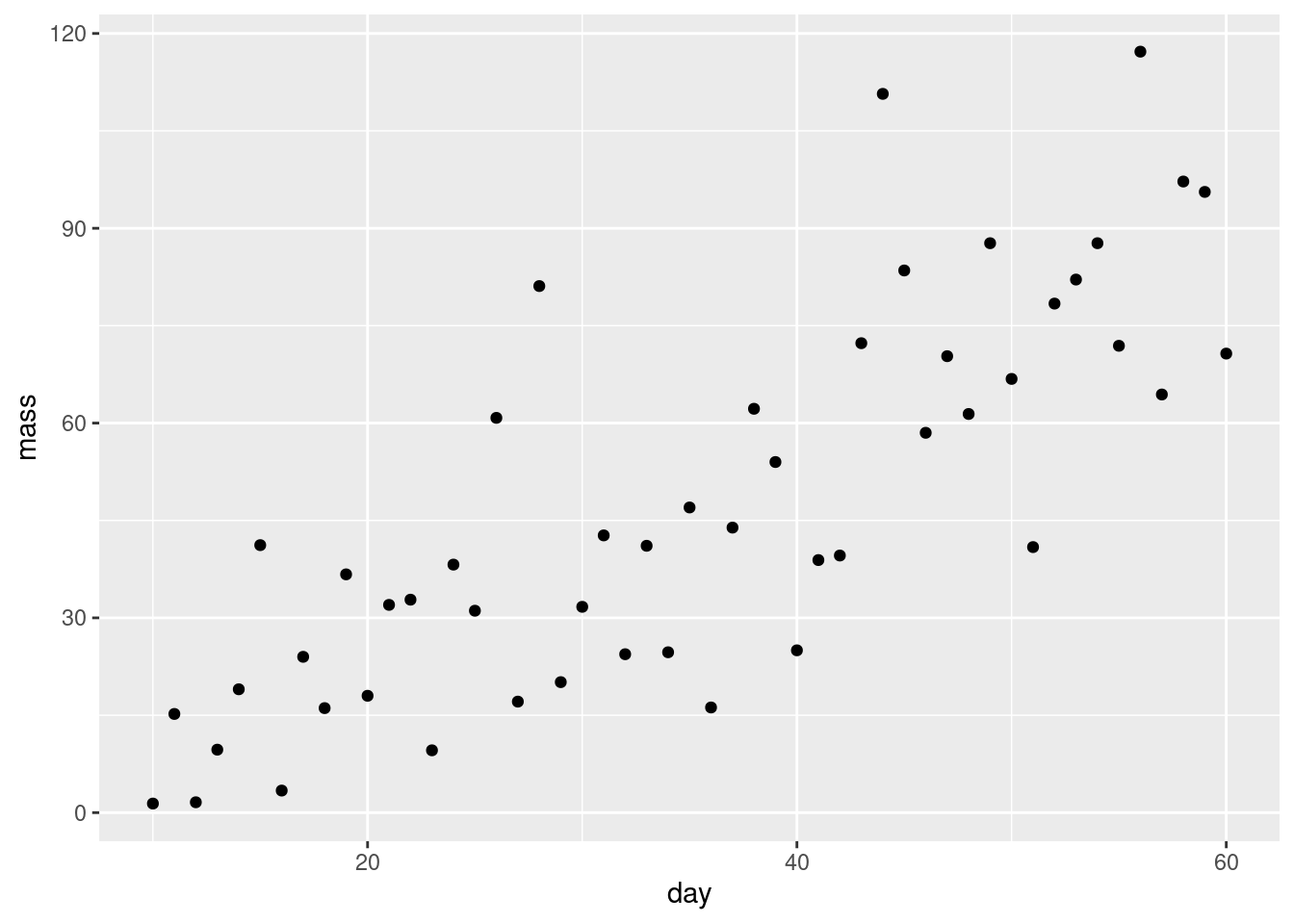
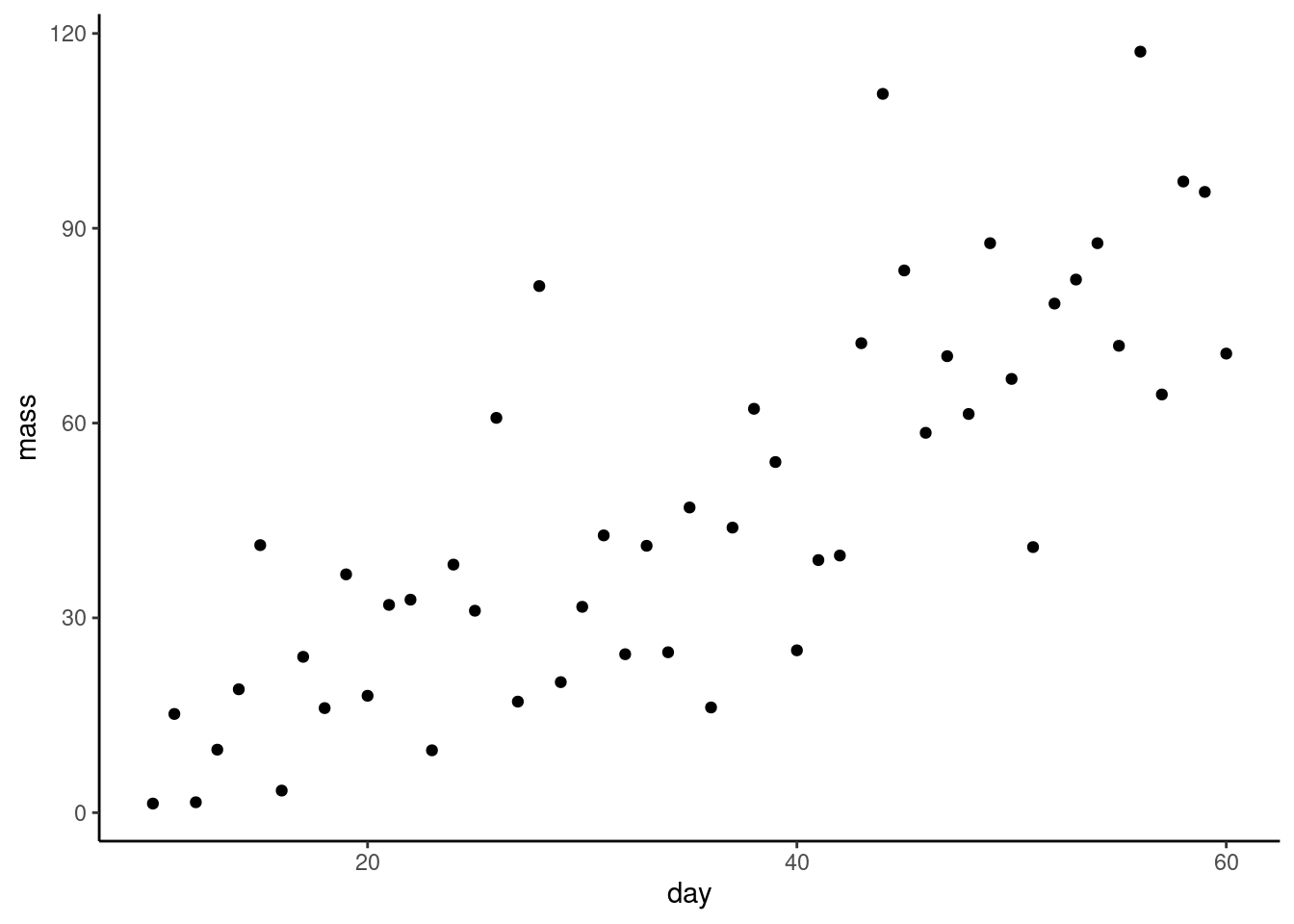
The data in plant.xlsx is a set of observations of plant growth over two months. The researchers planted the seeds and harvested, dried and weighed a plant each day from day 10 so all the data points are independent of each other.

Save a copy of plant.xlsx to your data-raw folder and import it.

What type of variables do you have? Which is the response and which is the explanatory? What is the null hypothesis?

Exploring

Do a quick plot of the data:

ggplot(plant, aes(x = day, y = mass)) +
  geom_point()

What are the assumptions of linear regression? Do these seem to be met?

Applying, interpreting and reporting

We now carry out a regression assigning the result of the lm() procedure to a variable and examining it with summary().

mod <- lm(data = plant, mass ~ day)
summary(mod)

Call:
lm(formula = mass ~ day, data = plant)

Residuals:
    Min      1Q  Median      3Q     Max 
-32.810 -11.253  -0.408   9.075  48.869 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  -8.6834     6.4729  -1.342    0.186    
day           1.6026     0.1705   9.401  1.5e-12 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 17.92 on 49 degrees of freedom
Multiple R-squared:  0.6433,    Adjusted R-squared:  0.636 
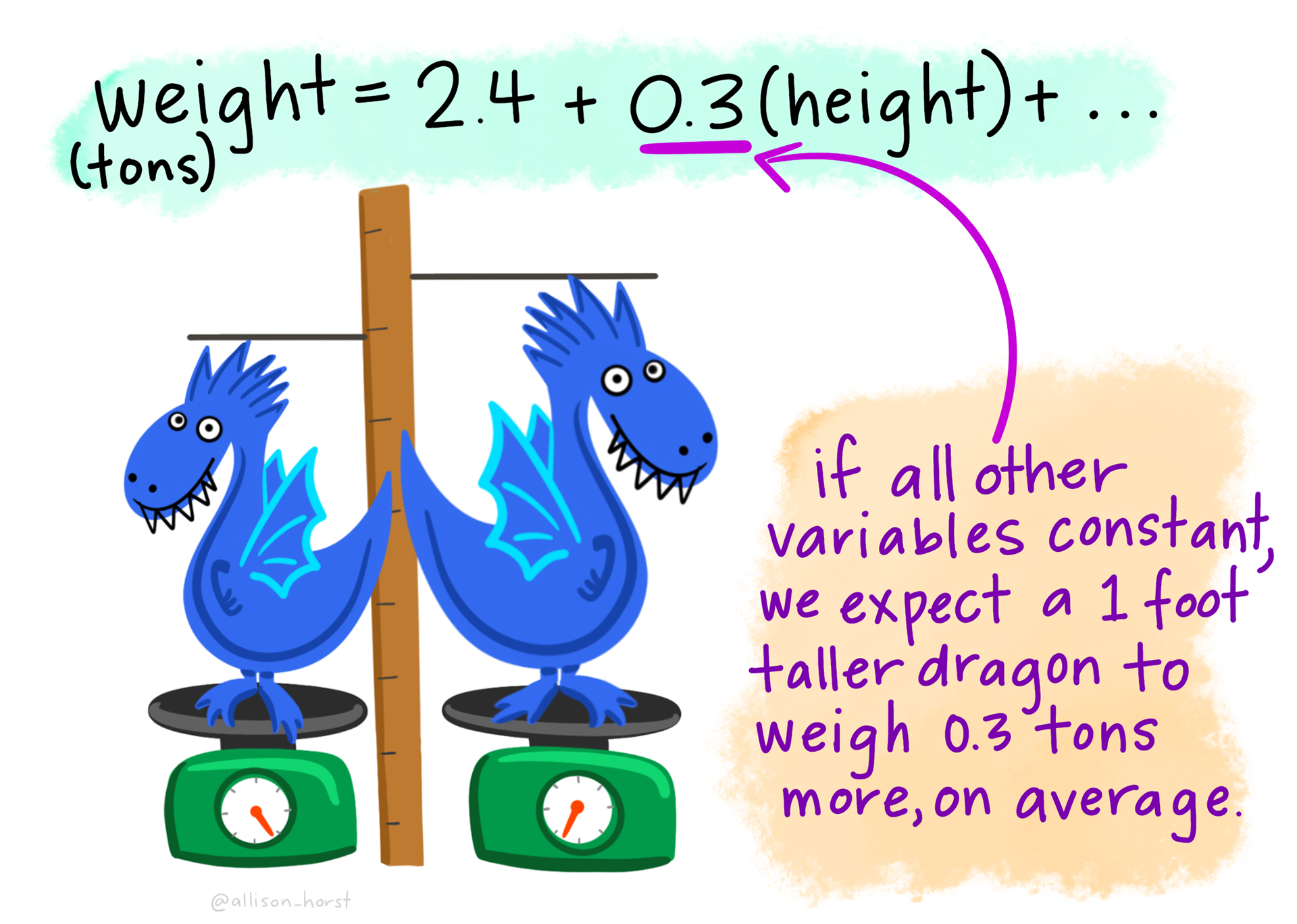
F-statistic: 88.37 on 1 and 49 DF,  p-value: 1.503e-12

The Estimates in the Coefficients table give the intercept (first line) and the slope (second line) of the best fitting straight line. The p-values on the same line are tests of whether that coefficient is different from zero.

The F value and p-value in the last line are a test of whether the model as a whole explains a significant amount of variation in the dependent variable. For a single linear regression this is exactly equivalent to the test of the slope against zero.

What is the equation of the line? What do you conclude from the analysis?

Does the line go through (0,0)?

What percentage of variation is explained by the line?

It might be useful to assign the slope and the intercept to variables in case we need them later. The can be accessed in the mod$coefficients variable:

mod$coefficients

(Intercept)         day 
  -8.683379    1.602606 

Assign mod$coefficients[1] to b0 and mod$coefficients[1] to b1:

b0 <- mod$coefficients[1] |> round(2)
b1 <- mod$coefficients[2] |> round(2)

I also rounded the values to two decimal places.

Checking assumptions

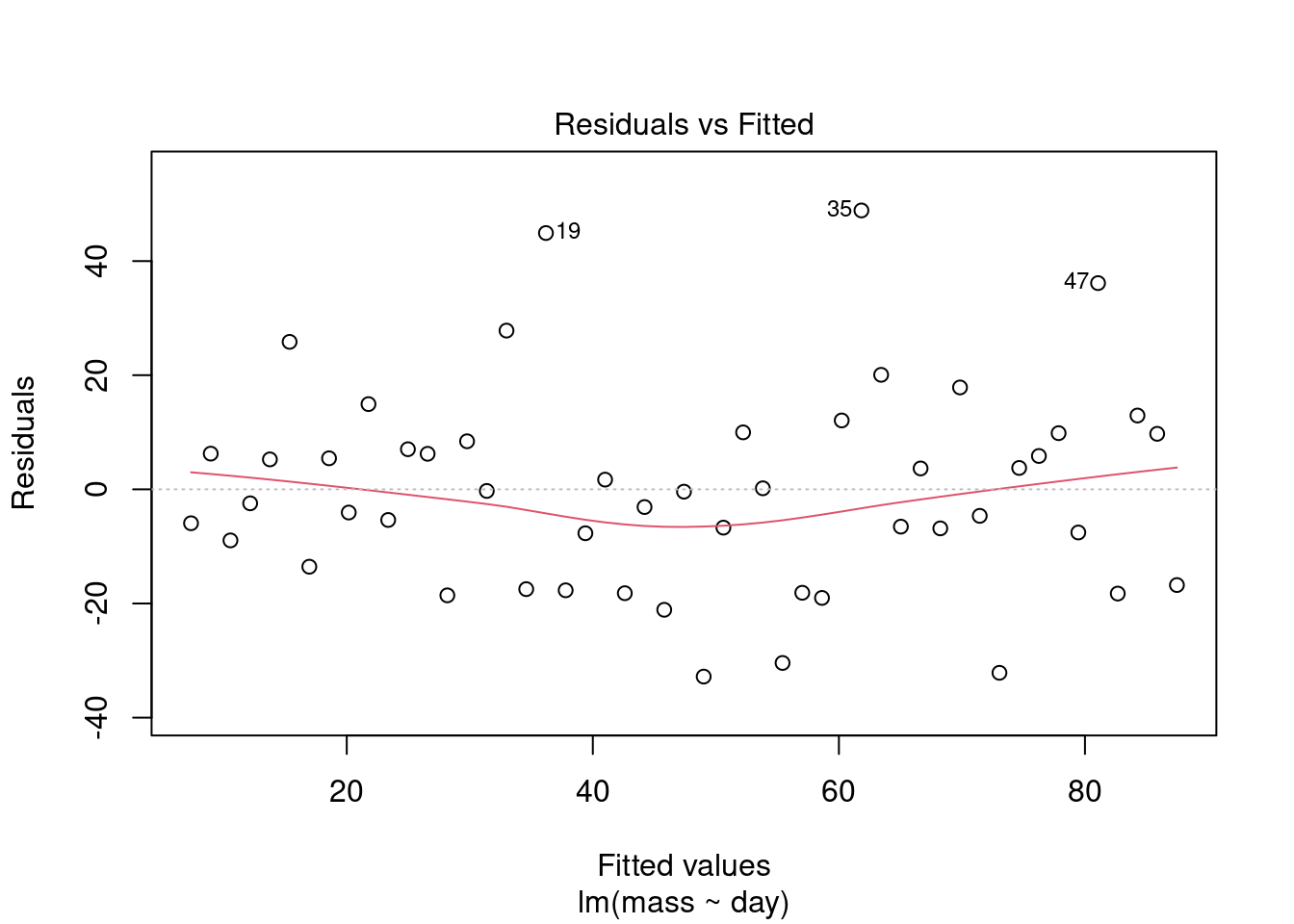
We need to examine the residuals. Very conveniently, the object which is created by lm() contains a variable called $residuals. Also conveniently, the R’s plot() function can used on the output objects of lm(). The assumptions demand that each y is drawn from a normal distribution for each x and these normal distributions have the same variance. Therefore we plot the residuals against the fitted values to see if the variance is the same for all the values of x. The fitted - predicted - values are the values on the line of best fit. Each residual is the difference between the fitted values and the observed value.

Plot the model residuals against the fitted values like this:

plot(mod, which = 1)

What to you conclude?

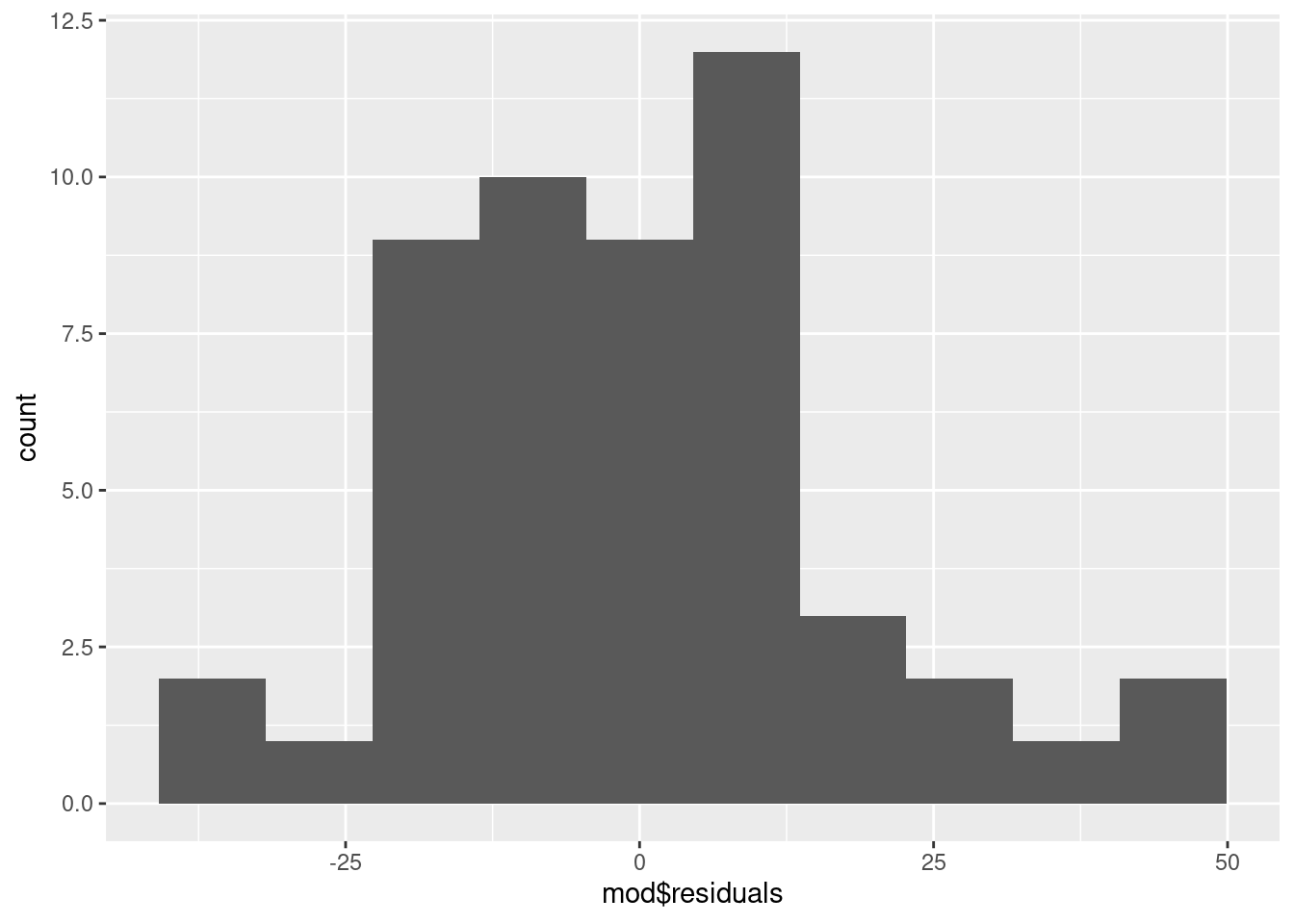
To examine normality of the model residuals we can plot them as a histogram and do a normality test on them.

Plot a histogram of the residuals:

ggplot(mapping = aes(x = mod$residuals)) + 
  geom_histogram(bins = 10)

Use the shapiro.test() to test the normality of the model residuals

shapiro.test(mod$residuals)

    Shapiro-Wilk normality test

data:  mod$residuals
W = 0.96377, p-value = 0.1208

Usually, when we are doing statistical tests we would like the the test to be significant because it means we have evidence of a biological effect. However, when doing normality tests we hope it will not be significant. A non-significant result means that there is no significant difference between the distribution of the residuals and a normal distribution and that indicates the assumptions are met.

What to you conclude?

Illustrating

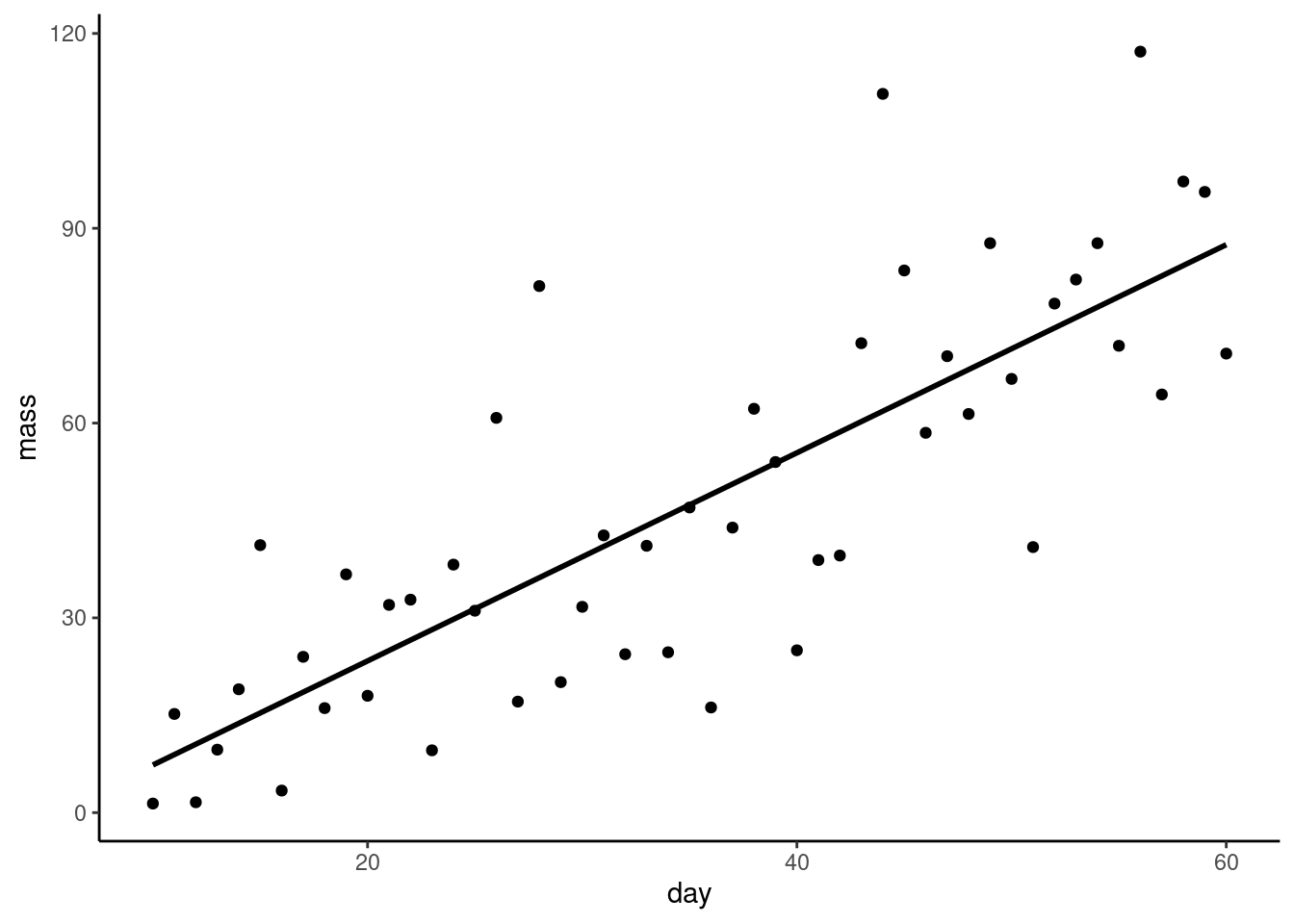
We want a figure with the points and the statistical model, i.e., the best fitting straight line.

Create a scatter plot using geom_point()

ggplot(plant, aes(x = day, y = mass)) +
  geom_point() + 
  theme_classic()

The geom_smooth() function will had a variety of fitted lines to a plot. We want a line so we need to specify method = "lm":

ggplot(plant, aes(x = day, y = mass)) +
  geom_point() +   
  geom_smooth(method = lm, 
              se = FALSE, 
              colour = "black") +
  theme_classic()

What do the se and colour arguments do? Try changing them.

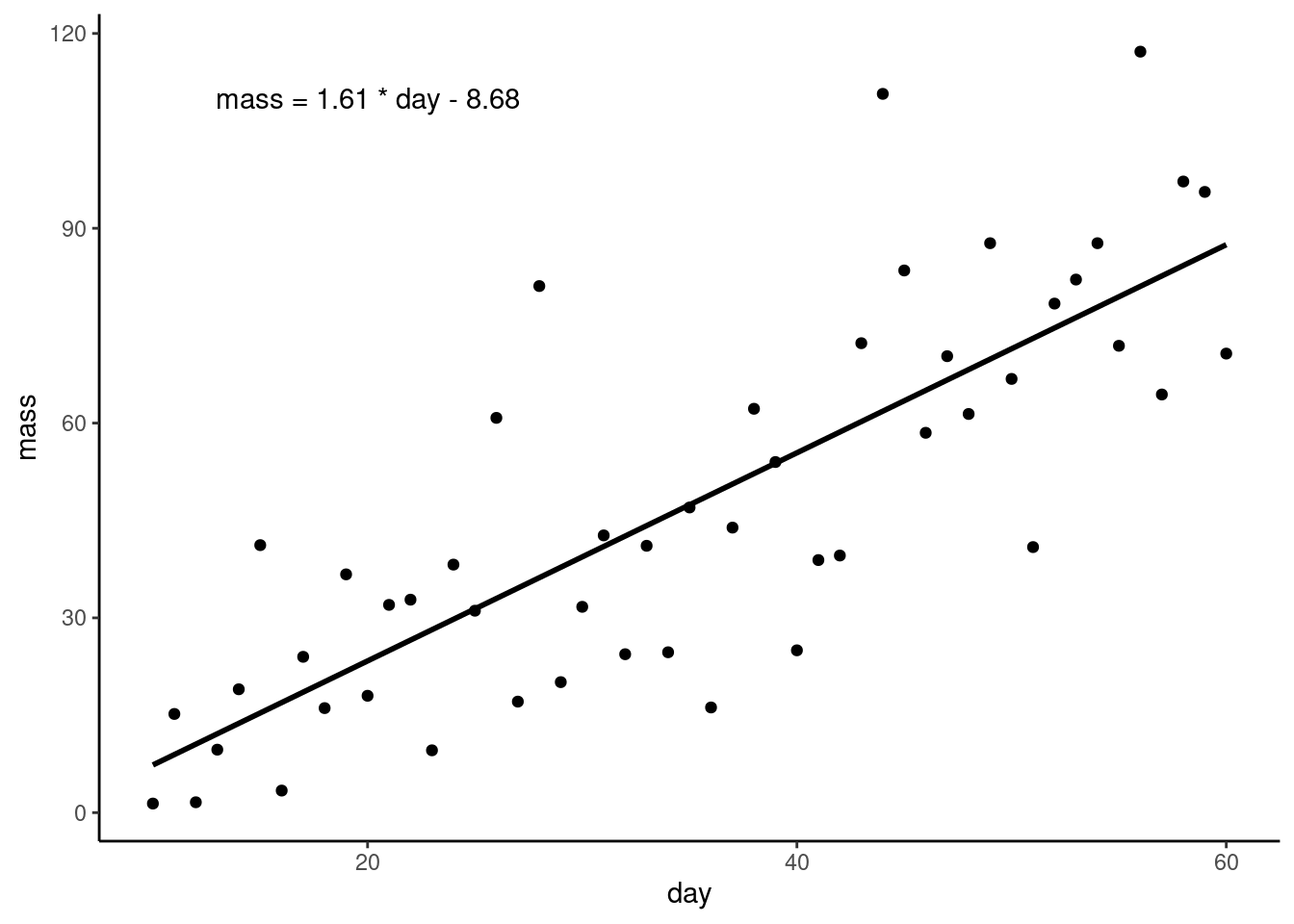
Let’s add the equation of the line to the figure using annotate():

ggplot(plant, aes(x = day, y = mass)) +
  geom_point() +
  geom_smooth(method = lm, 
              se = FALSE, 
              colour = "black") +
  annotate("text", x = 20, y = 110, 
           label = "mass = 1.61 * day - 8.68") +
  theme_classic()

We have to tell annotate() what type of geom we want - text in this case, - where to put it, and the text we want to appear.

Improve the axes. You may need to refer back Changing the axes from the Week 2 workshop

Save your figure to your figures folder.

Look after future you!

You’re finished!

🥳 Well Done! 🎉

Artwork by Horst (2023): “length typos”

Independent study following the workshop

Consolidate

The Code file

This contains all the code needed in the workshop even where it is not visible on the webpage.

The workshop.qmd file is the file I use to compile the practical. Qmd stands for Quarto markdown. It allows code and ordinary text to be interweaved to produce well-formatted reports including webpages. View the Qmd in Browser. Coding and thinking answers are marked with #---CODING ANSWER--- and #---THINKING ANSWER---

Pages made with R (R Core Team 2023), Quarto (Allaire et al. 2022), knitr (Xie 2022), kableExtra (Zhu 2021)

References

Allaire, J. J., Charles Teague, Carlos Scheidegger, Yihui Xie, and Christophe Dervieux. 2022. Quarto. https://doi.org/10.5281/zenodo.5960048.

Horst, Allison. 2023. “Data Science Illustrations.” https://allisonhorst.com/allison-horst.

R Core Team. 2023. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. https://www.R-project.org/.

Wickham, Hadley, Mara Averick, Jennifer Bryan, Winston Chang, Lucy D’Agostino McGowan, Romain François, Garrett Grolemund, et al. 2019. “Welcome to the Tidyverse” 4: 1686. https://doi.org/10.21105/joss.01686.

Xie, Yihui. 2022. “Knitr: A General-Purpose Package for Dynamic Report Generation in r.” https://yihui.org/knitr/.

Zhu, Hao. 2021. “kableExtra: Construct Complex Table with ’Kable’ and Pipe Syntax.” https://CRAN.R-project.org/package=kableExtra.